Динамические объекты управления большой размерности. Оптимальное управление линейными динамическими системами. Для определения элементов матриц, имеем систему алгебраических уравнений
Введение. Рыночная экономика в Украине требует новых подходов к управлению: на первый план выходят экономические, рыночные критерии эффективности. Научно-технический прогресс и динамика внешней среды заставляют современные производственные предприятия трансформироваться в более сложные системы, для которых необходимы новые методы управления. Усиление рыночной ориентации предприятий, резкие изменения внешней среды вызывают необходимость разработки конкурентоспособных систем управления, призванных вырабатывать комплексные управленческие решения, а следовательно и более эффективных подходов и алгоритмов решения задач большой размерности.
Работа выполнялась согласно государственной научно-технической программы 6.22 – перспективные информационные технологии и системы планы научной и научно-технической деятельности Одесского ордена Ленина института Сухопутных войск на 2004 год, соответственно к тематике научно-исследовательских работ.
Анализ последних исследований.В настоящее время одним из основных и наиболее эффективных подходов к решению задач управления большой размерности является декомпозиция . Этот подход объединяет группу методов, основанных на разложении исходной задачи большой размерности на подзадачи, каждая из которых существенно проще исходной и решается независимо от других. Связь между отдельными подзадачами осуществляется с помощью «координирующей» задачи, которая тоже проще исходной. Для этого задачу управления приводят к виду, удовлетворяющему требованиям декомпозируемости, основными из которых являются: аддитивность (сепарабельность) целевой функции; блочный характер ограничений; наличие блочных связей. Однако при решении практических задач синтеза оптимального управления большой размерности зачастую сложно удовлетворить перечисленным требованиям. Например, качество работы производственной системы может оцениваться критерием весьма общего типа, который может быть несепарабельным по отношению к задачам управления отдельными подсистемами. Поэтому при проведении исходной задачи управления к виду, удовлетворяющему требованиям декомпозируемости, неизбежны как различные упрощения, аппроксимации, так и различные варианты разбиения задачи на локальные подзадачи, т.е. блоков ограничений и межблочных связей. Все эти факторы влияют как на качество решения, так и на сложность расчетов при поиске оптимального решения.
Ввиду отсутствия до настоящего времени способов качественной оценки влияния перечисленных факторов на качество решения представляется актуальным разработка такого способа решения задачи большой размерности, который бы оставлял определенную свободу в выборе структуры локальных задач, а также удовлетворяющего и оценивающего влияние различных упрощений на качество решений.
Из анализа литературных источников следует, что приемлемые численные методы решения нелинейных задач оптимизации связаны со значительными затратами машинного времени и памяти, а использование линеаризации приводит к потерям качества управления. Поэтому целесообразно, чтобы разрабатываемый новый метод решения задачи сохранял её нелинейный характер, а оптимальное управление определялось в рамках децентрализованной вычислительной структуры.
Объектом исследования являются алгоритмы решения задач управления большой размерности.
Предметом исследований является разработка подхода, основанного на идее эквивалентности или квазиэквивалентности исходной задачи большой размерности и соответствующей блочной декомпозиционной задачи.
Научная задача состоит в разработке алгоритмов, использование которых обеспечивало бы оптимальное управление в рамках децентрализованной структуры, без необходимости итерационного обмена информацией между уровнями управления.
Целью работы является разработка и дополнение элементов прикладной теории и проблемно-ориентированного инструментария оптимизации задач управления большой размерности.
Научная новизна состоит в разработке подхода к синтезу алгоритмов оптимизации задач управления большой размерности в рамках децентрализованной вычислительной структуры, при которой отпадает необходимость в организации итерационного процесса между уровнями управления.
Основной материал. Пусть, рассматриваемая задача оптимального управления непрерывной динамической системой, определяется дифференциальным уравнением
(1)
по критерию
 (2)
(2)
![]() при
при
где - n m – мерный вектор управления; - n – мерная функция, составляющая которой непрерывно дифференцируемы относительно аргументов; - выпуклая, дифференцируемая скалярная функция; - заданные соответственно начальный и конечный момент времени.
С целью представления объекта управления (1) в виде ряда взаимодействующих подсистем разложим (1) в ряд Тейлора относительно точки равновесия
где ,
или
(3)
В выражении (3) А и В представляют собой блочно-диагональные части матриц и соответственно, с блоками и .
а и - недиагональные части и соответственно.
Введением вектора взаимосвязи таким образом, что задаваемая в i – тая составляющая определяется выражением
![]() ,
(4)
,
(4)
можно записать уравнение i – й подсистемы
где - - мерный вектор управления; - - мерный вектор состояния; - n – мерный вектор взаимосвязи.
Предлагаемый декомпозиционный способ синтеза оптимальных управлений состоит в следующем. Составляющую подсистему
и учитывающую взаимосвязь с другими подсистемами, назовем изолированной.
Композиция i – ых i = 1,2,…, Р подсистем представляет модель
(5)
где и - блочно – диагональные матрицы с блоками и соответственно.
Сформулируем критерий
 ,
(6)
,
(6)
где - положительно – полуопределенная блочно – диагональная матрица

с блоками ; - положительно – определенная блочно – диагональная матрица

с блоками , - оптимальное управление.
Матрицы и определим из условия квазиэквивалентности задач (1) – (2) и (5) – (6), которое имеет вид
здесь , ,
где
![]() .
.
Для определения элементов матриц, имеем систему алгебраических уравнений
![]() .
(7)
.
(7)
После решения уравнения (7) имеем Р независимых задач оптимизации в связи с блочно – диагональной структурой матриц
![]() ,
,
Локальное оптимальное управление имеет вид
![]() , (8)
, (8)
![]() , удовлетворяет
линейному дифференциальному уравнению .
, удовлетворяет
линейному дифференциальному уравнению .
, ![]() .
(9)
.
(9)
Глобальное решение является композицией оптимальных решений
![]() .
(10)
.
(10)
Выводы. Таким образом, задача синтеза оптимального управления для исходной задачи большой размерности (1) – (2) сводиться к следующему: формулировка локальных задач оптимизации (5) – (6); определение параметров локальных задач по формулам (3) и (6); решение локальных задач согласно (8) – (9); композиция локальных решений (10).
Потери качества при оптимальном подходе к синтезу приближенно оптимальных управлений можно оценить по формулам, предложенным в .
The new approach to problem solving of control, founded on idea of equivalence an initial problem of large dimension and conforming unitized offcomposite of a problem is offered.
1. Месарович М., Мако Д., Такахара И. Теория иерархических многоуровневых систем. – М.: Мир, 1973.
2. Аэсдон Л.С. Оптимизация больших систем. – М.: Мир, 1975.
3. Альбрехт Э.Г. Об оптимальной стабилизации нелинейных систем. – Прикладная математика и механика, 1961, т. 25.
4. Живоглядов В.П., Кривенко В.А. Способ декомпозиции задач управления большой размерности с несепарабельным критерием качества. Тезисы II Всесоюзной межвузовской конференции «Математическое, алгоритмическое и техническое обеспечение АСУ ТП». Ташкент, 1980.
5. Hassan Mohamed, Sinqh Madan G. The optimization for non – linear systemsusinq a new two level method. “Automatica”, 1976, 12, №4.
6. Mahmoud M.S. Dynamic multilevel optimization for a class of non – linear systems, “Int. J. Control”, 1979, 30, №6.
7. Кривенко В.А. Квазиэквивалентное преобразование оптимизационных моделей в задачах синтеза алгоритмов управления. – В кн.: Адаптация и оптимизация в больших системах. – Фрунзе, 1985.
8. Кривенко В.А. Способ синтеза алгоритмов управления с использованием идеи модификации целевой функции. – Фрунзе, 1985.
9. Румянцев В.В. Об оптимальной стабилизации управляемых систем. – Прикладная математика и механика, 1970, вып. 3.
10. Овезгельдыев А.О., Петров Э.Т., Петров К.Э. Синтез и идентификация моделей многофакторного оценивания и оптимизации. – К.: Наукова думка, 2002.
Ответы на вопросы
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ
Кафедра Физико-Математических Методов Управления
ЗАДАНИЯ
на курсовую работу
«Оптимальное управление линейными динамическими системами»
по курсу «Оптимальное управление»
Составитель: проф., д. т. н. Афанасьев В.Н.
Москва 2014
- ЦЕЛЬ РАБОТЫ
Математическое конструирование оптимальных линейных систем управления.
- СОДЕРЖАНИЕ РАБОТЫ
- Изучение необходимого теоретического материала по источникам ;
- Получение аналитического решения задачи;
- Составление структурной схемы системы управления.
- Приобретение навыков математического моделирования системы управления с использованием пакета MatLab .
- ВРЕМЯ ПРОВЕДЕНИЯ РАБОТЫ
VIII семестр, 4 курс.
Задания выдаются на 5 учебной неделе.
Прием выполненных работ осуществляется на 10 и 11 неделях.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ.
ФОРМУЛИРОВКА ЗАДАЧИ
Многие объекты управления могут достаточно точно описываться линейными динамическими моделями. Путем разумного выбора квадратичных критериев качества и квадратичных ограничений в этом случае удается синтезировать весьма удачные управляющие устройства с линейной обратной связью.
Пусть управляемые динамические системы, описываемые линейными дифференциальными уравнениями
(1)
здесь: - состояние системы; - управляющий вход системы; - выход системы. Таким образом, матрицы A (t ), B (t ), C (t ) имеют соответствующие размерности: n x n , n x r , m x n . Предположим, что и на управление не наложено каких-либо ограничений.
Определим назначение системы с физической точки зрения. Пусть - «желаемый» выход системы. Требуется отыскать такое управление u (t ) , при котором ошибка системы
(2)
была бы «малой».
Так как управление u (t ) в рассматриваемой задаче не ограничено, то для того чтобы избежать больших усилий в контуре управления и большого расхода энергии, можно ввести в критерий качества соответствующее требование, учитывающее эти факты.
Часто бывает важно сделать «малой» ошибку в конечный момент переходного процесса.
Перевод этих физических требований в форму того или иного математического функционала зависит от многих причин. В данной главе будет рассматриваться частный класс критериев качества, имеющих следующий вид:
(3)
где F , Q (t ) положительно полуопределенные матрицы размерностью m x m ; R (t ) положительно определенная матрица размерностью r x r .
Рассмотрим каждый член функционала (3). Начнем с. Очевидно, так как матрица Q (t ) положительно полуопределенная, то этот член неотрицателен при любом e (t ) и равен нулю при e (t )=0 . Так как, где q ij (t ) элемент матрицы Q (t ), а e i (t ) и e j (t ) компоненты вектора e (t ), то большие ошибки оцениваются «дороже», чем малые.
Рассмотрим член. Так как R (t ) - положительно определенная матрица, то этот член положителен при любых и «наказывает» систему за большие управляющие воздействия сильнее, чем за малые.
Наконец, . Этот член часто называют стоимостью конечного состояния. Его цель гарантировать «малость» ошибки в конечный момент времени переходного процесса.
Критерий качества (3) удобен математически, и его минимизация приводит к тому, что оптимальные системы оказываются линейными.
Задача оптимального управления формулируется следующим образом: дана линейная динамическая управляемая система (1) и функционал (3). Требуется найти оптимальное управление, т.е. управление, под воздействием которого система (1) двигается таким образом, чтобы минимизировать функционал (3). Поиск решений будет производиться для задач с открытой областью изменений управляющих воздействий и задач, управляющие воздействия в которых принадлежат заданному множеству.
- ЗАДАНИЕ
- Изучить метод построения оптимального управления линейными динамическими системами
- В соответствии с номером варианта взять условие задачи из приложения
- Проверить свойства управляемости и наблюдаемости
- Построить наблюдатель Луенбергера
- Получить аналитическое решение задачи
- Нарисовать структурную схему системы оптимального управления
- Изучить влияние весовых коэффициентов на качество переходных процессов и на значение функционала качества
- Математическое моделирование системы управления с использованием пакета MatLab
ПРИЛОЖЕНИЕ
Объект управления:
Функционал: .
Вариант № 1
Рассмотреть при:
- ;
Вариант № 2
Рассмотреть при:
- ;
Вариант № 3
Рассмотреть при:
- ;
Вариант № 4
Рассмотреть при:
- ;
Вариант № 5
Рассмотреть при:
- ;
Вариант № 6
Рассмотреть при:
- ;
Вариант № 7
Рассмотреть при:
- ;
Вариант № 8
Рассмотреть при:
- ;
Вариант № 9
Рассмотреть при:
- ;
Вариант № 10
Рассмотреть при:
- ;
Вариант № 11
Рассмотреть при:
- ;
Вариант № 12
Рассмотреть при:
- ;
Вариант № 13
Рассмотреть при:
- ;
Вариант № 14
Рассмотреть при:
14.1. ;
14.2. .
Вариант № 15
Рассмотреть при
15.1. ;
15.2. .
ЛИТЕРАТУРА
- Афанасьев В.Н., Колмановский В.Б., Носов В.Р. Математическая теория конструирования систем управления Высшая школа. М., 2003, 616 с.
- Афанасьев В.Н. Теория оптимального управления непрерывными динамическими системами. Аналитическое конструирование. М. Физический факультет МГУ 2011, 170 с.
- Афанасьев В.Н. Оптимальные системы управления. РУДН. 2007. − 260 с.
СПИСОК ЛИТЕРАТУРЫ
1. Попов Э.В. Экспертные системы реального времени [Электронный ресурс] // Открытые системы - 1995. - № 2. - Электрон. дан. - Режим доступа: http://www.osp.ru/text/302/178608/
2. Crossland R., Sims W.J.H., McMahon C.A. An object-oriented modeling framework for representing uncertainty in early variant design. // Research in Engineering Design - 2003. - № 14. -С. 173-183.
3. Landmark Graphics ARIES [Электронный ресурс] - Электрон. дан. - 2006. - Режим доступа: http://www.geographix.com/ps/vi-ewpg.aspx?navigation_id=1273
4. Schlumberger Merak [Электронный ресурс] - Электрон. дан. -2006. - Режим доступа: http://www.slb.com/content/servi-ces/software/valuerisk/index.asp
5. Gensim G2 [Электронный ресурс] - Электрон. дан. - 2006. -Режим доступа: - http://www.gensym.com/?p=what_it_is_g2
6. Thurston D.L., Liu T. Design Evaluation of Multiple Attribute Un-
der Uncertainty // Systems Automation: Research and Applications.
1991. - V. 1. - № 2. - P. 93-102.
7. Paredis C.J.J., Diaz-Calderon A., Sinha R., Khosla P.K. Composab-le Models for Simulation-Based Design // Engineering with Computers. - 2001. - № 17. - P. 112-128.
8. Силич М.П. Системная технология: объектно-ориентированный подход. - Томск: Том. гос. ун-т систем управления и радиоэлектроники, 2002. - 224 с.
9. Силич М.П., Стародубцев ГВ. Объектная модель выбора инвестиционных проектов разработки нефтегазовых месторождений. // Автоматизация, телемеханизация и связь в нефтяной промышленности. - 2004. - № 11. - С. 16-21.
10. Хабибулина Н.Ю., Силич М.П. Поиск решений на модели функциональных отношений // Информационные технологии
2004. - № 9. - С. 27-33.
11. Jess Rete Algorithm [Электронный ресурс] - Электрон. дан. -
2006. - Режим доступа: http://www.jessru-
les.com/jess/docs/70/rete.html
ИСПОЛЬЗОВАНИЕ УПРАВЛЕНИЙ ИЗБЫТОЧНОЙ РАЗМЕРНОСТИ ДЛЯ АВТОНОМИЗАЦИИ УПРАВЛЯЕМЫХ ВЫХОДОВ МНОГОМЕРНЫХ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
А.М. Малышенко
Томский политехнический университет E-mail: [email protected]
Систематизированы сведения о влиянии управлений избыточной размерности на автономизируемость выходов стационарных линейных динамических объектов, предложены алгоритмы синтеза обеспечивающих подобный эффект прекомпенсаторов и обратных связей по состоянию и выходу.
Введение
Проблема автономного (независимого) управления составляющими управляемого выхода объекта относится к числу особо важных в практическом плане задач при синтезе систем автоматического управления (САУ), пожалуй, для большинства многомерных по выходу объектов управления. Она нашла свое отражение во многих публикациях, в том числе и монографиях, в частности в .
Более детально проработаны вопросы автоно-мизации для линейных стационарных многомерных объектов. Чаще всего ставятся и решаются задачи автономизации (развязки) каждого из выходов объекта, причем не обладающего избыточной размерностью т вектора управления (ИРВУ). В связи с недостижимостью в принципе подобного решения для многих объектов указанного типа, эта задача модифицирована в более общую задачу построчной развязки, определяемую как задача Моргана , когда для объекта с р выходами необходимо определить р множеств из т>р управлений и соответствующий закон управления, при которых каждое из множеств влияет только на один выход. Тем самым решение определяется в классе САУ с избыточной размерностью вектора управления по
сравнению с размерностью вектора управляемых переменных.
Наряду с вышеуказанными постановками, задачи автономизации сформулированы и как задачи поблочной автономизации (развязки), когда обеспечивается независимость лишь между выходными координатами, входящими в разные их блоки, но не внутри этих блоков (групп), а также каскадной автономизации. В последнем случае зависимость выходных координат между собой носит «цепочный» характер (каждая последующая зависит только от предыдущих, но не последующих в установленном для них ряде). И в этих случаях решение задач автономизации часто требует избыточности в размерности вектора управления по сравнению с числом управляемых переменных.
Условия разрешимости задач автономизации
Решения задач автономизации обычно находятся в классе линейных прекомпенсаторов либо линейных статических или динамических обратных связей, причем для этих целей применяется как аппарат передаточных матриц (чаще всего), так и методы пространства состояний, структурный и геометрический подходы. Два последних
подхода удачно дополняют первые, так как фактически только с их помощью удалось установить большинство известных условий разрешимости задач автономизации [б], дать более глубокие интерпретации их решений.
При использовании для автономизации (развязки) выходов линейного многомерного объекта прекомпенсатора, т. е. регулятора, реализующего жесткое управление в функции задания ¡d(t) без обратной связи, его передаточная матрица Wy(s) выбирается из условия
Wœ(s) = Wo(s) -W y(s), (1)
где Wo(s) - передаточная матрица объекта управления, а Wx(s) - желаемая передаточная матрица синтезируемой системы, удовлетворяющая условиям ее развязки по выходам.
Используемой для этих целей линейной статической обратной связи соответствует алгоритм управления
u(t) = F x(t) + G /u(t), (2)
а динамической -
u (s) = F (s) x(s) + G fi(s). (3)
Указанные обратные связи реализуемы как с регулярным (матрица G обратима), так и с нерегулярным преобразованием задания ¡d(t) системы.
Согласно вышеуказанные динамические обратные связи могут быть определены как частный случай динамических расширений, дополняющих объект, описываемый системой уравнений в форме «вход-состояние-выход» вида
x (t) = Ax (t) + Bu (t), y(t) = C x (t),
ua (t) p _ xa (t)_
где ха (/) = иа (/), или обобщенным операторным уравнением
и (5) = Г(5) х(5") + О(5) ¡л(5).
Управление объектом с моделью вида по алгоритму (2) дает итоговую передаточную матрицу системы
Ж^) = С (51 - (А + В Г (5))) ~1ВО =
Ж0(5) . (1 - Г(5)(51 - А) -1 В)-1 О = Ж0(5) . Н(5), (4)
где Wo(s)=C(sI-AylB и #(£) - соответственно, передаточные матрицы объекта и прекомпенсатора, эквивалентного по эффекту обратной связи; I -единичная матрица размерности нхн.
Используемое в геометрическом подходе каноническое преобразование Морза g=(T,F,G,R,S) с обратимыми T,G,S передаточной матрицы Wo(s) объекта "Lo(C,A,B)
(A, B, C) ^ (T A + BF + R C)T,T ~lBG, SCT)
сводит Wo(s) к ее бикаузальным преобразованиям слева и справа вида
W0(s) ^ Bi(s)-W0(s)-B2(s), (5)
где B1(s) = S_1;
B 2(s) = -G.
Из (4) и (5) следует, что регулярные статическая
(2) и динамическая (3) обратные связи могут интерпретироваться как бикаузальные прекомпенса-ции, т. е. могут быть заменены эквивалентными им по эффекту бикаузальными прекомпенсаторами. По отношению ко второй справедливо и обратное утверждение, однако бикаузальный прекомпенса-тор H(s) реализуем согласно в виде эквивалентной линейной статической обратной связи лишь для объекта с Wo(s) минимальной реализации, причем тогда и только тогда, когда Wo(s) и H-1(s) - полиномиальные матрицы.
Из (5) можно также сделать вывод, что бикау-зальные прекомпенсаторы и соответствующие им регулярные статическая и динамическая обратные связи не могут изменить структуру системы на бесконечности и обусловленные ею свойства, в частности минимальные инерционности (запаздывания) автономных каналов управления. Эти изменения могут быть достигнуты лишь в классе нерегулярных алгоритмов управления.
Условия разрешимости задач автономизации связаны со структурными свойствами управляемых объектов, описываемыми их списками инвариантов. Причем, необходимый для этого набор определяется тем, какой алгоритм (компенсатор) планируется использовать для этих целей. Согласно для определения реализуемых развязывающих динамических обратных связей достаточно информации о вход-выходной структуре объекта, заложенной в его передаточной матрице или в минимальной части описания в пространстве состояний. Разрешимость этой задачи с использованием статической обратной связи по состоянию устанавливается по внутренней структуре объекта управления, в частности на основе исследования его системных матриц Розенброка или Кронекера или канонической декомпозиции Морза .
Построчно развязывающий выходы объекта пре-компенсатор согласно может быть определен из (1) тогда и только тогда, когда m>p, а матрицы [ Wo(s) : W(s)] и Wo(s) имеют одинаковую структуру формы Смита-Макмиллана на бесконечности.
Если передаточная матрица объекта имеет полный строчный ранг (необходимое условие построч-
ной развязки, обеспечиваемое лишь при т>р), то развязку может обеспечить прекомпенсатор с передаточной матрицей
где Wnoб(s) - обратная справа к W0(s) матрица, а к -такое целое число, которое делает Wn(s) собственной матрицей.
В доказано, что развязка с помощью регулярной статической обратной связи (2) возможна тогда и только тогда, когда возможна развязка с помощью регулярной динамической обратной связи
(3). В свою очередь, согласно , последнее возможно тогда и только тогда, когда бесконечная структура передаточной матрицы объекта является объединением бесконечных структур ее строк.
Регулярность обратных связей фактически предполагает отсутствие у объекта избыточности в размерности вектора управления (т=р). Поэтому, если развязка в этом случае не достижима, а управляемый объект имеет потенциальную ИРВУ, то для достижения автономности управления каждой из выходных величин целесообразно воспользоваться этой избыточностью либо какими-то конструктивными изменениями объекта управления предварительно добиться у него ИРВУ. Следует также иметь в виду, что и в ситуациях, когда т>р, регулярная обратная связь может не привести к желаемому результату, в то время как в классе нерегулярных прекомпенсаторов или тех же обратных связей он может быть получен. Например, у объекта с передаточной матрицей
Нерегулярным обратным связям соответствуют просто каузальные (строго собственные) преком-пенсаторы. Поэтому образуемые ими с объектом управления системы в общем случае не будут сохранять на бесконечности структуру управляемого объекта. Этим, в частности, можно воспользоваться для обеспечения устойчивости синтезируемой системы. Напомним, что еще в было доказано, что с помощью регулярной обратной связи развязка и устойчивость системы могут быть одновременно достигнуты тогда и только тогда, когда у объекта не существует неустойчивых инвариантных нулей взаимосвязи. Последними называют такие инвариантные нули £0(С,А,Б), которые не являются одно-
временно и инвариантными нулями строчных подсистем £;(С,А,Б). Здесь с, /е 1,р - /-я строка матрицы С объекта. Эти нули по условиям развязки обусловливают ограничения на выбор полюсов синтезируемой системы. При этом множество фиксированных (не допускающих произвольного назначения) полюсов развязанной по выходам системы должно обязательно включать все инвариантные нули взаимосвязи.
Таким образом, алгоритм управления в случае правых инвариантных нулей взаимосвязи в объекте необходимо выбирать из условия, что он способен будет внести необходимую по условиям устойчивости коррекцию в структурные свойства системы. Таковыми, как показано выше, и могут быть алгоритмы с нерегулярной обратной связью, реализуемые фактически в классе систем с ИРВУ.
Полного решения задачи развязки с помощью обратной связи для объектов с правыми инвариантными нулями взаимосвязи до сих пор не получено. В частности, для ее реализации со статической обратной связью необходимо, как следует из , сделать структуру максимального подпространства управляемости, содержащегося в КегС, достаточно богатой для возрастания бесконечной структуры до списка существенных порядков объекта. Последние характеризуют степень зависимости на бесконечности между отдельными выходами и всеми остальными и могут быть вычислены по формуле:
пгв =ХПг -Х Пг г=1 г=1
выходы не развязываемы с помощью регулярных обратных связей, но развязываемы статическим прекомпенсатором с передаточной матрицей
Здесь п - порядок бесконечного нуля системы s¡ в форме Смита-Макмиллана передаточной матрицы объекта. Первая сумма в (6) определяется для системы £0(С,А,Б) в целом, а вторая - для ЦС;,А,Б), где С / - матрица С без /-й строки. Указанные здесь существенные порядки определяют минимальную бесконечную структуру, которая может быть получена у развязанной системы.
Для динамической нерегулярной обратной связи в установлено лишь условие развязки, сводящееся к тому, что избыточность размерности вектора управления (т-р) должна быть больше или равна дефициту столбцового ранга в бесконечности матрицы интерактора W0(s), а последняя должна иметь полный строчный ранг. Указанный интерактор передаточной матрицы объекта W0(s) -это матрица, обратная к эрмитовой форме W0(s). Попутно заметим, что /-й существенный порядок объекта может быть определен через интерактор его передаточной матрицы и равен полиномиальной степени его -го столбца.
Общих решений для синтеза алгоритмов управления в классе САУ с ИРВУ даже для линейных объектов, которые обеспечивают автономизацию
их выходов, до сих пор не получено. Использование управлений избыточной размерности при решении задач построчной развязки (автономизации выходов) объекта является фактически необходи-
мым условием в тех случаях, когда управляемый объект не удовлетворяет условиям разрешимости этой задачи в классе бикаузальных прекомпенсато-ров и соответствующих им обратных связей.
СПИСОК ЛИТЕРАТУРЫ
1. Уонэм М. Линейные многомерные системы управления. - М.: Наука, 1980. - 375 с.
2. Rosenbrock H.H. State-space and multivariable theory. - London: Nelson, 1970. - 257 p.
3. Мееров М. В. Исследование и оптимизация многосвязных систем управления. - М.: Наука, 1986. - 233 с.
4. Малышенко А.М. Системы автоматического управления с избыточной размерностью вектора управления. - Томск: Изд-во Томского политехн. ун-та, 2005. - 302 с.
5. Commault C., Lafay J.F., Malabre M. Structure of linear systems. Geometric and transfer matrix approaches // Cybernetika. - 1991.
V. 27. - № 3. - P. 170-185.
6. Descusse J., Lafay J.F., Malabre M. Solution of Morgan’s problem // IEEE Trans. Automat. Control. - 1988. - V. aC-33. -P. 732-739.
7. Morse A.S. Structural invariants of linear multivariable systems // SIAM J. Control. - 1973. - № 11. - P. 446-465.
8. Aling H., Schumacher J.M. A nine fold canonical decomposition for linear systems // Int. J. Control. - 1984. - V. 39. - P 779-805.
9. Hautus M.L.J., Heymann H. Linear feedback. An algebraic approach // SIAM J. Control. - 1978. - № 16. - P. 83-105.
10. Descusse J., Dion J.M. On the structure at infinity of linear square decouplable systems // IEEE Trans. Automat. Control. - 1982. -V. AC-27. - P. 971-974.
11. Falb PL., Wolovich W. Decoupling in the design and synthesis of multi-variable systems // IEEE Trans. Automat. Control. - 1967. -V. AC-12. - P 651-669.
12. Dion J.M., Commault C. The minimal delay decoupling problem: feed-back implementation with stability // SIAM J. Control. -1988. - № 26. - P. 66-88.
УДК 681.511.4
АДАПТИВНЫЕ ПСЕВДОЛИНЕЙНЫЕ КОРРЕКТОРЫ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
М.В. Скороспешкин
Томский политехнический университет E-mail: [email protected]
Предложены адаптивные псевдолинейные амплитудный и фазовый корректоры динамических свойств систем автоматического регулирования. Проведено исследование свойств систем автоматического регулирования с адаптивными корректорами. Показана эффективность применения псевдолинейных адаптивных корректоров в системах автоматического регулирования с нестационарными параметрами.
В системах автоматического регулирования объектами, свойства которых изменяются с течением времени, необходимо обеспечить целенаправленное изменение динамических характеристик регулирующего устройства. В большинстве случаев это осуществляется изменением параметров пропорционально-интегрально-дифференциальных регуляторов (ПИД-регуляторов). Такие подходы описаны, например, в , однако реализация этих подходов связана либо с идентификацией, либо с использованием специальных методов, основанных на вычислениях по кривой переходного процесса. Оба эти подхода требуют значительного времени на подстройку.
В настоящей работе приводятся результаты исследования свойств систем автоматического регулирования с ПИД-регулятором и последовательными адаптивными амплитудным и фазовым псев-долинейными корректорами динамических характеристик. Такой способ адаптации характеризуется
тем, что в процессе работы системы регулирования параметры регулятора не меняются и соответствуют настройке, предшествующей запуску системы в работу. В процессе работы системы регулирования, в зависимости от типа используемого корректора, меняется коэффициент передачи корректора или создаваемый им фазовый сдвиг. Эти изменения происходят только в тех случаях, когда возникают колебания регулируемой величины, связанные с изменением свойств объекта управления или из-за воздействия на объект управления возмущений. А это позволяет обеспечить устойчивость системы и повысить качество переходных процессов.
Выбор псевдолинейных корректоров для реализации адаптивной системы объясняется следующим. Корректоры, используемые для изменения динамических свойств систем автоматического регулирования, можно разбить на три группы: линейные, нелинейные и псевдолинейные . Основной недостаток линейных корректоров связан с
В рассмотренных примерах (задача о загрузке рюкзака и задача о надежности) для описания состояний системы использовалась только одна переменная, одной переменной задавалось и управление. В общем случае в моделях динамического программирования состояния и управления могут быть описаны с помощью нескольких переменных, образующих вектора состояния и управления.
Увеличение количества переменных состояния вызывает рост числа возможных вариантов решения, ассоциированных с каждым из этапов. Это может привести к так называемой проблеме «проклятие размерности», которая является серьезным препятствием при решении задач динамического программирования средней и большой размерности.
В качестве примера рассмотрим задачу о загрузке рюкзака, но уже при двух ограничениях (например, ограничение по весу и по объему):
где , . Поскольку в задаче имеется два вида ресурсов , то необходимо ввести два параметра состояния и . Обозначим , , . Тогда ограничения (1) можно привести к виду:
где . В рекуррентных уравнениях метода динамического программирования для задачи о «ранце» с двумя ограничениями (1):
каждая из функций , является функцией двух переменных. Если каждая из переменных , может принимать 10 2 значений, то функцию приходится табулировать в 10 4 точках. В случае трех параметров при тех же предположениях требуется вычислять 10 8 степени значений функций .
Итак, наиболее серьезным препятствием практического применения динамического программирования оказывается число параметров задачи.
Задача управления запасами.
Задача управления запасами возникает, когда необходимо создать запас материальных ресурсов или предметов потребления с целью удовлетворения спроса на заданном интервале времени (конечном или бесконечном). В любой задаче управления запасами требуется определять количество заказываемой продукции и сроки размещения заказов. Спрос можно удовлетворить путём однократного создания запаса на весь рассматриваемый период времени или посредством создания запаса для каждой единицы времени этого периода. Первый случай соответствует избыточному запасу по отношению к единице времени, второй – недостаточному запасу по отношению к полному периоду времени.
При избыточном запасе требуется более высокие удельные (отнесённые к единице времени) капиталовложения, но дефицит возникает реже и частота размещения заказов меньше. С другой стороны, при недостаточном запасе удельные капитальные вложения снижаются, но частота заказов и риск дефицита возрастают. Для любого из указанных крайних случаев характерны значительные экономические потери. Таким образом, решения относительно размера заказа и момента его размещения могут основываться на минимизации соответствующей функции общих затрат, включающих затраты, обусловленные потерями от избыточного запаса и дефицита.
Эти затраты включают в себя:
1. Затраты на приобретение, которые становятся особо важным фактором, когда цена единицы выражается в виде оптовых скидок в тех случаях, когда цена единицы продукции убывает с возрастанием размера заказа.
2. Затраты на оформление заказа представляют собой постоянные расходы, связанные с его размещением. При удовлетворении спроса в течении заданного периода времени путём размещения более мелких заказов (более часто) затраты возрастают по сравнению со случаем, когда спрос удовлетворяется посредством размещения более крупных заказов (и следовательно, реже).
3. Затраты на хранение запаса, которые представляют собой расходы на содержание запаса на складе (процент на инвестированный капитал, амортизационные расходы и эксплуатационные расходы), обычно возрастают с увеличением уровня запасов.
4. Потери от дефицита, обусловленные отсутствием запаса необходимой продукции. Обычно они связаны с экономическими санкциями со стороны потребителей, потенциальными потерями прибыли. На рис.1 иллюстрируется зависимость рассмотренных видов затрат от уровня запаса продукции. На практике какую-либо компоненту затрат можно не учитывать, если она не составляет существенную часть общих затрат. Это приводит к упрощению моделей управления запасами.
Типы моделей управления запасами.
Большое разнообразие моделей управления запасами определяется характером спроса на продукцию, который может быть детерминированным или вероятностным. На рис.2 приведена схема классификации спроса, принимаемая в моделях управления запасами.
Детерминированный статический спрос предполагает, что интенсивность потребления остаётся неизменной во времени. Динамический спрос - спрос известен, но изменяется в зависимости от времени.
Наиболее точно характер спроса может быть описан посредством вероятностных нестационарных распределений. Однако с математической точки зрения модель значительно усложняется, особенно при увеличении рассматриваемого периода времени.
По существу классификацию на рис.2 можно считать представлением различных уровней абстракции описания спроса.
На первом уровне предполагается, что распределение вероятностей спроса стационарно во времени, т.е. в течение всех исследуемых периодов времени используется одна и та же функция распределения вероятностей. При таком предположении влияние сезонных колебаний спроса в модели не учитывается.
На втором уровне абстракции учитываются изменения спроса от одного периода к другому. Однако при этом функции распределения не применяются, а потребности в каждом периоде описываются средней величиной спроса. Это упрощение означает, что элемент риска в управлении запасами не учитывается. Но оно позволяет исследовать сезонные колебания спроса, которые вследствие аналитических и вычислительных трудностей нельзя учесть в вероятностной модели.
На третьем уровне упрощения предполагается, что спрос в течении любого периода равняется среднему значению известного спроса по всем рассматриваемым периодам, т.е. оценить его постоянной интенсивностью.
Характер спроса является одним из основных факторов при построении модели управления запасами, но имеются и другие факторы, влияющие на выбор типа модели.
1. Запаздывание поставок. После размещения заказа он может быть поставлен немедленно или потребуется некоторое время на его выполнение. Интервал времени между моментом размещения заказа и его поставкой называется запаздыванием поставки. Эта величина может быть детерминированной или случайной.
2. Пополнение запаса. Процесс пополнения запасов может осуществляться мгновенно или равномерно во времени.
3. Период времени определяет интервал, в течение которого осуществляется регулирование уровня запаса. В зависимости от отрезка времени, на котором можно надёжно прогнозировать запас, рассматриваемый период принимается конечным или бесконечным.
4. Число пунктов накопления запасов. В систему управления запасами может входить несколько пунктов хранения запаса. В некоторых случаях эти пункты организованы таким образом, что один выступает в качестве поставщика для другого. Эта схема иногда реализуется на различных уровнях так, что пункт – потребитель одного уровня может стать пунктом – поставщиком на другом. В этом случае имеется система управления с разветвлённой структурой.
5. Число видов продукции. В системе управления запасами может фигурировать более одного вида продукции. Этот фактор учитывается при условии наличия некоторой зависимости между видами продукции. Так, для различных изделий может использоваться одно и тоже складское помещение или же их производство может осуществляться при ограничениях на общие производственные фонды.
Детерминированные модели управления запасами.
1.Детерминированная обобщённая модель определения оптимального размера партии продукции при допущении дефицита.
Рассматривается система управления запасами, когда продукция поступает на склад непосредственно с производственной линии с постоянной интенсивностью единиц продукции в единицу времени. При достижении некоторого уровня объёма запаса Q производство продукции прекращается. Возобновление производства и поставки продукции на склад осуществляется в момент, когда неудовлетворённый спрос достигнет некоторого значения G. Расходование запаса осуществляется с интенсивностью . Известны значения следующих параметров: - стоимость хранения единицы товара на складе в единицу времени; -стоимость организации заказа (одной партии продукции); - убытки от неудовлетворенного спроса (штраф). Требуется найти оптимальный объём партии продукции и интервал времени между точками возобновления поставки по критерию минимума общих затрат от функционирования системы управления запасами.
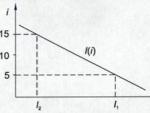
Графически условия задачи показаны на рис.3.
Из рисунка видно, что пополнение и расходование запаса осуществляются одновременно в течение интервала каждого цикла. Накопленный запас Q полностью расходуется в течение интервала . В течение интервала спрос не удовлетворяется, а накапливается. Неудовлетворённый спрос G покрывается в интервале .
Величина называется полным циклом управления запасом. - предельный запас продукции, G – предельный дефицит продукции.
Очевидно текущий уровень запаса продукции определяется по формуле:
Из треугольника OAB следует:
Аналогично можно определить , и (2)
Из подобия треугольников OAC и CEF можно записать Из равенства следует, что (3)
Выражение (3) с учётом (1) перепишется:
Тогда общая сумма затрат на пополнение, хранение запаса продукции и возможный штраф за неудовлетворительный спрос будет определяться выражением:
Если привести затраты в единицу времени, то выражение для удельных затрат будет иметь вид:
Таким образом, есть функция двух аргументов Q и T, оптимальные значения которых определяются как решение задачи:
Для того, чтобы найти минимум функции двух аргументов, необходимо и достаточно решить систему уравнений:
Это следует из факта, что функция является вогнутой функцией относительно своих аргументов. Решение системы уравнений (5) даёт следующие неотрицательные корни:
Минимум общих затрат в единицу времени составит:
Можно рассмотреть частные случаи.
1. Дефицит продукции не допускается. Решение задачи в этом случае получается из формулы (6)-(8), если положить штраф Тогда С 1 /С 3 =0 и оптимальные значения искомых величин будут:
Этому случаю соответствует график изменения уровня запаса во времени:
2. Пополнение запаса осуществляется мгновенно. В этом случае полагается и соответственно
График изменения уровня запаса имеет вид:
3. Дефицит не допускается, запасы пополняются мгновенно, т.е. . Тогда следует:
Эти формулы называются формулами Уилсона, а величина - экономическим размером партии.
График изменение уровня запаса имеет вид:
Динамические модели управления запасами.
В предыдущих лекциях были рассмотрены статические задачи управления запасами за один период. В ряде таких задач были получены аналитические выражения для оптимального уровня запаса.
В случае, если рассматривается функционирование системы за n периодов, причем спрос непостоянен, приходят к динамическим моделям управления запасами. Эти задачи, как правило, не поддаются аналитическому решению, однако оптимальные уровни запасов на каждый период можно вычислить, применив метод динамического программирования.
Рассматривается задача управления запасами, когда спрос за j-ый период (j=1,n) определяется величиной . Пусть – уровень запаса в начале j-го периода, а - объем пополнения запаса в этом периоде. Пополнение запасов осуществляется мгновенно в начале периода, дефицит продукции не разрешается. Графически условия задачи показаны на рис.1.
Пусть - общие затраты на хранение и пополнение на j-том периоде. Значение задано, а , т.к. в конце функционирования систем запас не нужен.
Требуется определить оптимальные объемы заказов в каждом периоде по критерию минимума суммарных затрат.
Математическая модель задачи будет иметь вид
здесь необходимо определить , которые удовлетворяли бы ограничениям (2)-(6) и минимизировали целевую функцию (1).
В этой модели целевая функция сепарабельная, ограничения (2) имеют рекуррентный вид. И эта особенность модели наталкивает на мысль о возможности применения для ее решения метода динамического программирования. Модель (1)-(6) отличается от стандартной модели динамического программирования наличием условия это условие можно преобразовать следующим образом. Из (2) и (3) следует, что , или можно записать
Тогда из (7) с учетом (4) определяется область возможных значений : или окончательно:
Таким образом, условие (3)-(4) заменяется условием (8), и модель (1),(2),(5)-(6),(8) имеет стандартный вид для метода динамического программирования.
В соответствии с методом динамического программирования решение этой задачи состоит из следующих этапов:
Иследует из ограничения (12)-(14).(j=2,n).
Проводится обратное движение алгоритма, в результате находятся оптимальные значения искомых переменных и . Минимальное значение целевой функции (1) определяется величиной
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С.П.КОРОЛЕВА»
Ю. Заболотнов
ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ НЕПРЕРЫВНЫМИ ДИНАМИЧЕСКИМИ СИСТЕМАМИ
Утверждено Редакционно-издательским советом университета в качестве учебного пособия
САМАРА 2005
УДК 519.9+534.1
Рецензенты: С.А. Ишков, Л.В. Кудюров
Заболотнов Ю.
Оптимальное управление непрерывными динамическими системами: учеб. пособие / Ю. Заболотнов ; Самар. гос. аэрокосм. ун-т. Самара, 2005. 149 с. : ил.
Пособие включает в себя описание методов оптимального управления динамическими системами. Особое внимание уделено оптимальному решению задачи стабилизации для линейных динамических систем. Наряду с изложением классических методов оптимального управления линейными системами, основанными главным образом на принципе динамического программирования Беллмана, рассматривается приближенно оптимальное управление колебательными динамическими системами с использованием метода усреднения.
Материал пособия входит в курс лекций «Теоретические основы автоматизированного управления», читаемых автором для студентов специальности 230102 – автоматизированные системы обработки информации и управления на кафедрах информационных систем и технологий, математики и механики СГАУ. Однако пособие может быть полезно для студентов других специальностей при изучении теории оптимального управления динамическими системами.
ПРЕДИСЛОВИЕ ……………………………………………………. 5
1. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ДИНАМИЧЕСКИМИ СИСТЕМАМИ ………………………….………………………….. 8
1.1. Постановка задачи оптимального управления динамическими системами …………………………….…...8
1.2. Программное оптимальное управление и задача
стабилизации ………………………………………………………. 11
1.3 . Невозмущенное и возмущенное движения динамической системы …………………………………………….………….. 12
1.4. Постановка задачи оптимальной стабилизации движения для линейной динамической системы.……………………………..… 14
2. УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ
ДИНАМИЧЕСКИХ СИСТЕМ ………………………………….….16
2.1. Подобные преобразования линейных динамических систем.16
2.2. Управляемость динамических систем.……………………….18
2.3. Наблюдаемость динамических систем ……………………….21
3. ПРИНЦИП ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ БЕЛЛМАНА И ТЕОРИЯ УСТОЙЧИВОСТИ ЛЯПУНОВА …….24
3.1. Принцип динамического программирования Беллмана …….24
3.2. Оптимальное управление линейными динамическими системами ………………………………………………..………… 29
3.3. Теория устойчивости Ляпунова ………………………………31
3.4. Связь метода динамического программирования с теорией устойчивости Ляпунова …………………………………………... 37
4. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ДЛЯ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ …………………… 39
4.1. Решение уравнения Беллмана для линейных стационарных динамических систем..…………………………………………… 39
4.2. Решение уравнения Беллмана для линейных нестационарных динамических систем..…………………………………………… 41
4.3. О выборе критерия оптимальности при решении задачи стабилизации ……………………………………………………….43
4.4. Пример оптимального выбора коэффициентов регулятора
при управлении линейной системой второго порядка....……….. 47
5. ДИНАМИЧЕСКИЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ ………….56
5.1. Малые колебания динамических.истем…………………….…56
5.2. Управляемость и наблюдаемость линейных колебательных динамических систем ………………………………………………. 65
5.3. Метод малого параметра..…………………………………….. 68
5.4. Метод усреднения..………………………………………….… 72
5.5. Метод усреднения для системы с одной степенью свободы.. 76
5.6. Метод усреднения для систем с несколькими быстрыми
фазами ………………………………………………………………. 79
5.7. Метод усреднения для системы с двумя степенями
свободы ………………………………………………………..…… 86
6. ПРИБЛИЖЕННО ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ДИНАМИЧЕСКИМИ КОЛЕБАТЕЛЬНЫМИ СИСТЕМАМИ.... 93
6.1. Управление линейной колебательной системой с одной степенью свободы ……………………………………………….… 93
6.2. Управление линейной колебательной системой с двумя степенями свободы..………………………………………………. 106
6.3. Влияние нелинейных возмущений на решение задачи оптимального управления …………//…………………………… 115
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ …..…………127
ПРИЛОЖЕНИЕ 1. Подобные преобразования линейных динамических систем …………………………………………..…129
ПРИЛОЖЕНИЕ 2. Качественное исследование линейных динамических систем на фазовой плоскости …………………… 134
ПРИЛОЖЕНИЕ 3. Дифференцирование функций с векторным аргументом ………………………………………………………... 142
ПРИЛОЖЕНИЕ 4. Основные понятия теории асимптотических рядов ………………………………………………………………. 143
ПРИЛОЖЕНИЕ 5. Усреднение тригонометрических
функций ………………………………………..………………….. 148
ПРЕДИСЛОВИЕ
Традиционно в классической теории управления рассматриваются две основные задачи: задача определения программного движения динамической системы и задача о проектировании регуляторов, реализующих заданное программное движение объекта управления (задача стабилизации). Основное внимание в пособии уделяется решению задачи стабилизации, при решении которой обычно используются линейные динамические модели. По сравнению со статическими системами в динамических системах процесс развивается во времени и управление в общем случае тоже является функцией времени.
При решении задачи стабилизации могут быть использованы различные методы. Здесь, прежде всего, следует отметить классические методы теории автоматического управления, основанные на аппарате передаточных функций и частотных характеристик. Однако появление быстродействующих ЭВМ привело к развитию новых методов, составляющих основу современной теории управления. В современной теории управления поведение системы описывается в пространстве состояний и управление системой сводится к определению оптимальных в некотором смысле управляющих воздействий на систему в каждый момент времени. Причем математическими моделями непрерывных динамических систем обычно являются системы обыкновенных дифференциальных уравнений, независимой переменной в которых является время.
При решении задачи стабилизации оптимальность управления понимается в смысле минимума некоторого критерия оптимальности (функционала), который записывается в виде определенного интеграла. Критерий оптимальности может характеризовать различные аспекты качества управления: затраты на управление (энергии, топлива и др.), ошибки управления (по различным переменным состояния) и т.д. Для определения оптимального управления при решении задачи стабилизации используется классический принцип динамического программирования Беллмана.
Первый раздел пособия является вводным: в нем производится математическая постановка задач, решаемых при управлении непрерывными динамическими системами. Второй раздел посвящен вопросам, предваряющим построение оптимального управления для линейных систем: вопросам управляемости и наблюдаемости. В третьем разделе выводятся основные соотношения принципа динамического программирования Беллмана, из которых далее определяется оптимальное управление для линейной динамической системы при решении задачи стабилизации. В этом же разделе показывается, что принцип динамического программирования Беллмана для линейных систем органически связан со вторым методом Ляпунова, выполнение теорем которого обеспечивает решение задачи стабилизации. В четвертом разделе пособия излагаются алгоритмы определения оптимального управления при решении задачи стабилизации при заданном квадратичном критерии оптимальности (подынтегральная функция функционала является квадратичной формой от управления и переменных состояния системы). Приводится пример определения оптимального управления с заданным критерием оптимальности для конкретной линейной системы. В пятом разделе излагаются основы теории динамических колебательных систем. Выводятся основные соотношения принципа усреднения, позволяющего во многих случаях существенно упростить анализ и синтез колебательных систем. В шестом разделе рассматривается метод определения приближенно оптимального управления для задачи стабилизации колебательными системами. Приводятся примеры управления колебательными системами с одной и с двумя степенями свободы. Анализируются вопросы возможного влияния нелинейных возмущений на решение задач стабилизации колебательных систем.
Методы, изложенные в пособии, позволяют найти оптимальное управление для решения задач стабилизации динамических систем в виде аналитических функций, зависящих от переменных состояния системы. В этом случае говорят, что решается задача синтеза управления. Эти методы можно отнести к теории аналитического конструирования регуляторов, являющейся одной из важных направлений развития современной теории управления.
Материал пособия основывается на работах в области теории управления, которые с течением времени уже стали классическими. Здесь прежде всего необходимо отметить работы Понтрягина Л.С. , Летова А.М. , Демидовича Б.П. , Гропа Д. , Беллмана Р. , Моисеева Н.Н., Боголюбова Н.Н., Митропольского Ю.А. и др. известных отечественных и зарубежных ученых.
1. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ДИНАМИЧЕСКИМИ СИСТЕМАМИ
1.1. Постановка задачи оптимального управления динамическими системами
Математические модели динамических систем могут быть построены в различных формах. Это могут быть системы обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, соответствующие дискретные модели и др. Отличительной особенностью математического описания любой динамической системы является то, что ее поведение развивается во времени и характеризуется функциями ,… , которые называются переменными состояния (фазовыми координатами) системы. В дальнейшем будем рассматривать системы с непрерывным временем. Движение динамической системы может быть управляемым и неуправляемым. При реализации управляемого движения поведение динамической системы зависит также от управляющих функций ,… . Предположим также, что поведение системы определяется однозначно, если задана вектор-функция управления и начальное фазовое состояние , где - начальное время.
В качестве математической модели динамической системы будем рассматривать систему обыкновенных дифференциальных уравнений, записанную в нормальной форме Коши
где , , - известная вектор-функция.
К системе (1.1) чаще всего приводятся разнообразные математические модели динамических систем с непрерывным временем. Так, например, если поведение динамической системы описывается системой дифференциальных уравнений в частных производных и происходит в пространстве и во времени (математические модели механики сплошной среды), то, производя дискретизацию по пространству (конечно элементный подход), приходим к системе обыкновенных дифференциальных уравнений подобной (1.1), решение которой ищутся как функции времени.
Введенное ранее предположение об однозначности процесса управления для системы (1.1) определяется выполнением условий теоремы о существовании и единственности решений систем обыкновенных дифференциальных уравнений в форме Коши .
Сформулируем задачу оптимального управления системой (1.1) . В начальный момент система (1.1) находится в состоянии , необходимо определить такое управление , которое переведет систему в заданное конечное состояние (отличное от начального), где - конечное время. Обычно требуется, чтобы переход из точки в точку (переходный процесс) был в определенном смысле наилучшим из всех возможных переходов. Например, если рассматривается некоторая техническая система, то переходный процесс должен удовлетворять условию минимума затраченной энергии или условию минимума времени перехода. Такой наилучший переходный процесс принято называть оптимальным процессом.
Функция управления обычно принадлежит некоторой области управления , которое является множеством -мерного евклидова пространства. В технических приложениях предполагают, что область есть замкнутая область, то есть область, включающая свои границы. Допустимым управлением будем называть любое управление , переводящее систему из точки в точку . Для количественного сравнения различных допустимых управлений вводят критерий оптимальности, который, как правило, представляют в виде некоторого функционала
Функционал вычисляется на решениях системы (1.1) , удовлетворяющих условиям и , при заданном допустимом управлении .
Окончательно, задача оптимального управления формулируется следующим образом: в фазовом пространстве даны две точки и ; среди всех допустимых управлений , переводящих фазовую точку из положения в положение , найти такое, для которого функционал (1.2) принимает наименьшее значение.
Управление , дающее решение поставленной выше задачи, называется оптимальным управлением и обозначается , а соответствующая траектория - оптимальной траекторией.
Замечание. Если необходимо обеспечить максимум некоторого критерия, то можно свести данную задачу к задаче поиска минимума формально изменив знак перед функционалом (1.2).
Частным случаем поставленной задачи оптимального управления является случай, когда . Тогда функционал (1.2) принимает вид и оптимальность заключается в реализации минимального времени перехода из точки в точку . Такую задачу оптимального управления называют задачей быстродействия.
1.2. Программное оптимальное управление и задача стабилизации
Рассмотрим движение динамической системы (1.1). Пусть для этой системы найдено оптимальное управление и получена соответствующая оптимальная траектория . При реализации оптимальной траектории в технических задачах неизбежно наталкиваются на существенные трудности, заключающиеся в невозможности, во-первых, точно установить реальную систему (или объект управления) в начальное состояние , во-вторых, точно реализовать само оптимальное управление , в третьих, точно предсказать заранее внешние условия функционирования системы (приближенность исходной математической модели). Все это приводит к необходимости решать задачу о коррекции закона оптимального управления в процессе функционирования любой технической системы (или объекта). Таким образом, задачу оптимального управления в реальных условиях можно разделить на две части: 1) построение номинального оптимального управления исходной динамической системой в идеальных условиях в рамках математической модели (1.1); 2) построение корректирующих управляющих воздействий с целью реализации заданного номинального оптимального управления и оптимальной траектории в процессе функционирования системы. Первую часть задачи оптимального управления принято называть задачей построения оптимального программного управления , причем она решается в рамках априорной информации, известной заранее о рассматриваемой системе. Вторую часть задачи называют задачей стабилизации заданной номинальной программы управления и решаться она должна в процессе функционирования системы по информации, поступающей от измерительных устройств системы управления. Задача стабилизации номинальной программы управления тоже может быть поставлена как задача поиска оптимального управления по соответствующему критерию, что будет сделано ниже (см. раздел 1.4).
Замечание. Очевидно, что в качестве номинальной программы управления может быть использована не только оптимальное управление , но и любое другое допустимое управление (если задача оптимизации программного управления не решается). В частном самом простом случае может быть, например, поставлена задача о стабилизации некоторого постоянного положения системы .
1.3. Невозмущенное и возмущенное движения динамической системы
Так как реальное движение системы неизбежно отличается от номинального программного, то этот факт привел к концепции невозмущенного и возмущенного движений Ляпунова А.А. . Так, любое программное движение системы (1.1), независимо от того является ли оно оптимальным или допустимым называется невозмущенным движением. Причем этому движению соответствует некоторое частное решение системы (1.1). Возмущенное движение оценивается при этом некоторыми отклонениями от невозмущенного движения. Следовательно, возмущенное движение будет описываться следующими переменными
где переменные и характеризуют номинальную программу управления, а переменные и - отклонения от номинальной программы.
Подставляя соотношения (1.3) в систему (1.1), получим
Прибавляя и отнимая в правой части системы (1.4) одинаковое слагаемое и учитывая, что
получим систему в отклонениях от номинального движения
где , , а определяются в результате решения системы (1.5).
Обычно считают, что отклонения и от номинального движения являются малыми величинами. Поэтому, если разложить функцию в ряд Тейлора и ввести обозначения , , где индекс (o) означает, что частные производные определяются для заданной номинальной программы, то получим
Здесь функция определяет слагаемые второго порядка и выше по отклонениям ; матрицы и выделяют линейную часть ряда и имеют компоненты и ; .
Уравнения, записанные в отклонениях (1.7), имеют большое значение в теории управления. На основании этих уравнений производится постановка большого количества задач оптимизации, имеющих практический интерес. Одна из этих задач – задача стабилизации, сформулированная выше. При решении этой задачи требуется определить, как следует выбрать корректирующие управляющие воздействия , чтобы уменьшить отклонения в некотором смысле наилучшем образом.
1.4. Постановка задачи оптимальной стабилизации движения для линейной динамической системы
Чаще всего при решении задачи стабилизации движения системы или объекта управления используется линейная динамическая система в отклонениях, получающаяся из системы (1.7) отбрасыванием нелинейных слагаемых . Тогда
где матрицы и в общем случае являются функциями времени, так как зависят от номинальной программы управления . , причем, то говорят, что решается задача синтеза управления. После подстановки закона. Рассмотрим случай, когда матрица не имеет кратных (одинаковых) собственных значений. В этом случае подобное преобразование приводит матрицу к диагональному виду , где - диагональная матрица, на главной диагонали которой стоят собственные значения матрицы (доказательство приводится в Приложении 1).

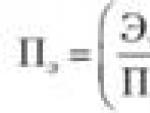




 «Потребительский экстремизм» или как защититься от недобросоветсных потребителей - Любовь Доронина Потребительский экстремизм статья
«Потребительский экстремизм» или как защититься от недобросоветсных потребителей - Любовь Доронина Потребительский экстремизм статья Сценка по литературе. Литературный сценарий. Примерные роли в сценке
Сценка по литературе. Литературный сценарий. Примерные роли в сценке Сценки на новый год смешные и прикольные
Сценки на новый год смешные и прикольные Сборник стихов для подготовишек
Сборник стихов для подготовишек